Neural Network Hardware Implemenation
Hardware Implementation of an MLP Neural Network Model in System Verilog.
Table of contents
About
This documentation contains the contents of my initial, midterm, and final report for my Neural Network Hardware Implementation design project for ECEN4303 in which I recieved an A+. I created a hardware implementation of a MLP (Multi-layer Percepton) feedforward neural network in System Verilog.
These reports will showcase my design choices, changing between a CNN (Convolutional Neural Network) and MLP, and the final results of the project including code and structure.
Towards the end of the project, I made the decision to change to an MLP model. This choice was made because of time constraints on designing a convolutional model in system verilog. This will be shown throughout the documentation below.
Initial Report
Introduction
This project’s purpose is to create a deeper fundamental understanding of integrated circuit design and artificial intelligence development, more specifically neural network design. The goal of this project is to create a hardware implementation of a neural network using Verilog in Model Sim. The task for this neural network is to accurately guess handwritten singledigit numbers trained using the MNIST 1-9 dataset. Broken down into 4 stages in respective order, I will be researching artificial intelligence and related theories to aid in completion, creating a python coded example of a convolutional neural network (CNN) to gather weights and biases, creating Verilog implementations of sub-modules that will be used in the full Verilog implementation, and finally combining the results of the previous steps into implementing the CNN and weights and biases into Verilog.
The recommended model type for this is a multilayer perceptron model but, for the challenge and some extra fun, I will be attempting to complete this using a 2-dimensional convolutional neural network (2D-CNN). I have a bit of experience developing neural networks for at-home projects including CNN classification models. My hope is to be successful in creating a hardware implementation of these networks for this class.
General Neural Networks
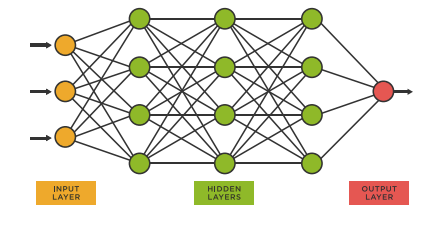
Neural networks are at the core of deep learning algorithms, artificial intelligence, and machine learning. These networks are created mostly in code and can be trained and deployed into applications to aid in the workplace, at home, and to overall increase the productivity and leisure of humans in society. Most commonly neural networks contain 3 stages, pictured below: input layer, hidden layers, and an output layer.
2D Convolutional Neural Networks
Convolutional neural networks are a type of neural network that are most used in image classification because of its speed and accuracy using a high number of inputs. There are 4 parameters/stages of a convolutional layer that are individually crucial to its accuracy and speed: Kernel filter, stride, padding, and pooling. The kernel filter size, N by N, is the size of the convolutional filter. The stride is the linear movement distance of the filter from convolution to convolution. Padding is a method of increasing the size of the input matrix by N in both dimensions to increase accuracy in each convolution. Finally, the pooling layer is responsible for reducing the spatial size of the convolved feature (this helps reduce the required computational power).
Pictured below, the input values are mapped to the output using a 2 by 2 kernel filter. The weight, 0.5, is applied to each input during the convolution/filtering process. The bias, b, is added to the final solution and calculated internally in the training process.
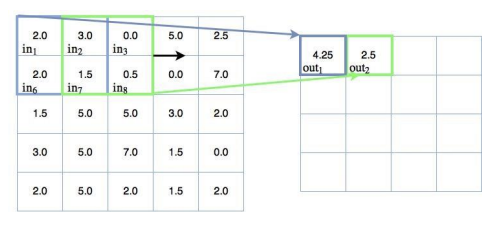
The equations below show the weight and bias being applied to each input to solve for the output:
𝑜𝑢𝑡1 = 0.5𝑖𝑛1 + 0.5𝑖𝑛2 + 0.5𝑖𝑛3 + 0.5𝑖𝑛4 + 𝑏 = 4.25
𝑜𝑢𝑡2 = 0.5𝑖𝑛2 + 0.5𝑖𝑛3 + 0.5𝑖𝑛7 + 0.5𝑖𝑛8 + 𝑏 = 2.5
Midterm Report
Introduction
The purpose of this midterm report is to reflect on everything that I have completed since the beginning of this project. I will overview each completed task and lightly evaluate methods and theories used in the process. The biggest accomplishment, and what this report will mostly outline, is the completion of the python implementation of my 2-dimensional convolutional neural network (2d-CNN). The rest of the report will simply describe the development and potential future integration of specific sub-modules that I have created in Verilog: The 16-bit ripple-carry, 16-bit bit-array multiplier, and ReLU (Rectified Linear Unit) Method. Note, I will not go into heavy detail on the theory behind a 2d-CNN, as this was explained in my initial report.
Python Implementation
The development of the python code implementation of a convolutional neural network started with research on how to effectively port the MNIST 0-9 integer dataset into PyTorch. Shown below, I was able to create loaders for the data to be used later in the training and testing methods of this program:
# MNIST Dataset and loaders
train_data = datasets.MNIST(root = 'data', train = True, transform = ToTensor(), download = True)
test_data = datasets.MNIST(root = 'data', train = False, transform = ToTensor())
loaders = {
'train' : DataLoader(train_data, batch_size=100, shuffle=True,
num_workers=1),
'test' : DataLoader(test_data, batch_size=100, shuffle=True, num_workers=1),
}Once this was completed, the design of the convolutional neural network was the next crucial step. The network is comprised of 3 core layers: Two 2-D convolutional layers (Each paired with a Rectified Linear Unit function porting to a 2-D Max Pooling Function) and a linear output layer. The network is then assigned a cross entropy loss function and Adam optimizer that are crucial to training the weights and biases of each layer noted previously. Shown below is the python code for the layers of the neural network as well as comments describing each layer’s parameters and design:
# Kernel Size = 5*5
# Stride = 1
# Padding = 2
# First convolution layer
# Input Size = 1 (Grayscale image, 1 dimensional color)
# Output Size = 16
#
# - nn.Sequential pairs each layer linearly to allow the
# output of each layer is the input for the next. (Conv2d --> ReLU --> MaxPool2d)
# - Simply, a tighter way of packaging layers together
self.convOne = nn.Sequential(nn.Conv2d(1, 16, 5, 1, 2), nn.ReLU(), nn.MaxPool2d(2))
# Second convolution layer
# Input Size = 16 (Output from convOne is 16)
# Output Size = 32
self.convTwo = nn.Sequential(nn.Conv2d(16, 32, 5, 1, 2), nn.ReLU(), nn.MaxPool2d(2))
# Linear output layer
# Input Size = 32 * (5 + 2) * (5 + 2) [Flattens total size of image pixels, including + 2 padding]
# Number of Classes = 10 (0-9 integers)
self.out = nn.Linear(32 * 7 * 7, 10)
# Cross Entropy Loss Function
self.loss_func = nn.CrossEntropyLoss()
# Adam Optimizer
# Learning Rate = 0.01
self.optimizer = optim.Adam(self.parameters(), lr = 0.01)
# Sends model to specified device (cuda or cpu)
self.to(device)Unexpectedly, due to a Nvidia CUDA driver error for my graphics card, I was forced to train the network on the CPU which was an extremely slow process. Using 10 epochs with a step size of 100, I was able to get an accuracy of 99% for this design of a convolutional neural network. I believe this accuracy is the effect of using a CNN instead of an MLP as they tend to be more accurate. This accuracy will also allow me some wiggle room for my Verilog implementation as it is bound to be less accurate. After training, the outputs of the weights and biases of each core layer will be written to a text file that will later be integrated into my Verilog layers in Phase 4. The entirety of this code base will be provided in my final report.
Verilog Sub-Modules
Unfortunately, due to time constraints, I was unable to fully complete the 16-bit ripplecarry, 16-bit bit-array multiplier, and ReLU (Rectified Linear Unit) Method in Verilog. The premise behind these parts are crucial for the continuation of this project, specifically the final phase. The adders and multipliers will be used as core components for the 2-D convolutional layers and the pooling phases. The equation below, for a convolution, is where the adders and multipliers will be used:
𝑜𝑢𝑡 = 𝑤1𝑖𝑛1 + 𝑤2𝑖𝑛2 + 𝑤3𝑖𝑛3 + 𝑤4𝑖𝑛4 + ⋯ + 𝑤𝑛𝑖𝑛𝑛 + 𝑏
The weights (w) and biases (b) will be imported from the final model of the python implementation in phase 2.
Final Report
Introduction
The end goal of this project is to create a Verilog implementation of a Multilayer Perceptron Neural Network Model. There are four key phases leading up to this goal: Research, python implementation, Verilog sub-module creation, and the final implementation in Verilog. My original take on this project was to create a Convolutional Neural Network, but due to time constraints and a lack of prior experience with Verilog, I was forced to switch back to the MLP design. Because of this, I will outline some elementary theory behind the MLP in the early stages of the project as only CNNs were stated in earlier reports.
Worth noting, this project is incomplete. I was unable to debug my neuron and layers successfully. Although this is the case, I do believe the code base is strong and that I was extremely close to finishing completely if I were to solve these errors. I will outline the issues that I ran into when trying to fully integrate the code base as well as potential problems that may have caused these issues.
Research (Phase 1)
The first phase of this project was to research the theory and methods behind an MLP neural network model. An MLP, Multilayer Perceptron, model is a basic type of feedforward neural network. They contain a hidden layer, output layer, activation function, optimizer, and loss function for training the weights and biases in the layer.
Once trained, the weights and biases will be assigned to each input and used to estimate the resulting output. Below is the summation equation used in a MLP layer:
𝑜𝑢𝑡 = 𝑤1𝑖𝑛1 + 𝑤2𝑖𝑛2 + 𝑤3𝑖𝑛3 + 𝑤4𝑖𝑛4 + ⋯ + 𝑤𝑛𝑖𝑛𝑛 + 𝑏
Python Implementation (Phase 2)
The second phase of this project was the python implementation. This was by far the easiest part of the project for me as I already have over a year of experience working with libraries like PyTorch to create neural network classification models. I decided to only use two layers in my model: One hidden layer followed by an output layer. The sizing of these layers is up to the user and can be tuned accordingly depending on the results of the training/testing.
Attached below is an image of the two layers along with the forward feed method that contains the ReLU activation function:
# Input size: 784 (28*28)
# Output size: 120
self.fc1 = nn.Linear(28*28, 120)
# Input size: 120
# Output size: 10
self.fc2 = nn.Linear(120, 10)
def forward(self, input):
# Flattens input to 1*748
x = input.view(-1, 28*28)
# ReLU activation function, max(0, x)
x = F.relu(self.fc1(x))
# Output
output = self.fc2(x)
return output, x The weights and biases of each layer were outputted in decimal floats which is not very applicable in simulation. I am sure I am not the only student that has done this, but I decided to convert these values to 32-bit hexadecimal fixed points before writing them to their respective text files for Verilog. This way I can easily use them in my adder and multiplier modules later in the project. Below is sample code of performing this conversion on the weights and biases:
Weights
def toHex(num, bits):
return hex((num + (1<<bits)) % (1<<bits))
for i in weights:
if abs(i) < 0.001:
if i < 0:
i = -0.001
else:
i = 0.001
# Using the fxpmath and toHex methods to turn the decimal floats into
# 32 bit hexadecimal fixed point values
final = toHex(Fxp(i, n_int=16, n_frac=16, signed=True).raw(), 32)
# Cleans up the output, adds 0's to the beginning if it is not a full
# 8 hex digits in length
final = str(final).replace("0x", "")
if (len(final) < 8):
for i in range(8 - len(final)):
final = "0" + str(final)
weights_file.write("{}\n".format(final))Biases
for i in biases:
if abs(i) < 0.001:
if i < 0:
i = -0.001
else:
i = 0.001
final = toHex(Fxp(i, n_int=16, n_frac=16, signed=True).raw(), 32)
final = str(final).replace("0x", "")
if (len(final) < 8):
for i in range(8 - len(final)):
final = "0" + str(final)
biases_file.write("{}\n".format(final))The rounding of decimals that are less than 0.001 could lead to potential inaccuracies, but the hex conversion that I was using failed if the number was too small which led me to do this. The full python code base is included in the zip file that will be turned in along with this report.
Verilog Sub-Modules (Phase 3)
For the third phase, the goal was to create different sub-modules that will be used in the final phase of the project. For the adders and multipliers, I chose to use carry look ahead methodology. These types of adders and multipliers are much faster than their counter parts, and when handling large amounts of input data, I felt this was necessary for this project.
ReLU
I also created the ReLU activation function during this time. This was an easy module to make because it is simply a maximum function:
𝑟𝑒𝑠𝑢𝑙𝑡 = max (0, 𝑖𝑛𝑝𝑢𝑡)
module relu (in, out);
input [31:0] in;
output [31:0] out;
// If the last bit is zero, then the result is positive and
// the output is the input.
// Else the result is negative and the output is zero.
assign out = (in[31] == 0)? in : 0;
endmoduleCLA Adder
The CLA Adder submodule was used to add the biases to the dot product of the weights and inputs:
module cla_adder (in1, in2, carry_in, sum, carry_out);
input [31:0] in1;
input [31:0] in2;
input carry_in;
output [31:0] sum;
output carry_out;
wire [31:0] gen;
wire [31:0] pro;
wire [32:0] carry_tmp;
genvar j, i;
generate
assign carry_tmp[0] = carry_in;
for(j = 0; j < 32; j = j + 1) begin: carry_generator
assign gen[j] = in1[j] & in2[j];
assign pro[j] = in1[j] | in2[j];
assign carry_tmp[j+1] = gen[j] | pro[j] & carry_tmp[j];
end
assign carry_out = carry_tmp[32];
for(i = 0; i < 32; i = i+1) begin: sum_without_carry
assign sum[i] = in1[i] ^ in2[i] ^ carry_tmp[i];
end
endgenerate
endmoduleCLA Multiplier
The CLA Multiplier submodule was used for the multiplication of the weights and inputs:
module cla_multiplier (multicand, multiplier, product, final);
input [31:0] multicand;
input [31:0] multiplier;
output [63:0] product;
output [31:0] final;
wire [31:0] multicand_tmp [31:0];
wire [31:0] product_tmp [31:0];
wire [31:0] carry_tmp;
genvar j, i;
generate
for(j = 0; j < 32; j = j + 1) begin: for_loop_j
assign multicand_tmp[j] = multicand & {32{multiplier[j]}};
end
assign product_tmp[0] = multicand_tmp[0];
assign carry_tmp[0] = 1'b0;
assign product[0] = product_tmp[0][0];
for(i = 1; i < 32; i = i + 1) begin: for_loop_i
cla_adder add1 (
.sum(product_tmp[i]),
.carry_out(carry_tmp[i]),
.carry_in(1'b0),
.in1(multicand_tmp[i]),
.in2({carry_tmp[i-1],product_tmp[i-1][31-:31]}));
assign product[i] = product_tmp[i][0];
end
assign product[63:32] = {carry_tmp[31],product_tmp[31][31-:31]};
endgenerate
wire [63:0] temp = product;
assign final[31:0] = temp[31:0];
endmoduleFile Reader
The file reader module was created to read the weights and biases files easily. This was, for some reason, the hardest part of the project for me. I decided to read and insert the hex values from the file into a hexadecimal variable with a length equal to that of the number of hex values in the file. To do this, I had to use a bit operation called splicing. Below is the file reading and splicing method that I used to gather the data based on the file name:
while(! $feof(wb_file)) begin
for (i = 0; i < size*count; i = i + 1) begin
$fscanf(wb_file, "%h\n", temp);
A[32*(i) +: 32] = temp[31:0];
end
endVerilog Implementation (Phase 4, Final)
Initial Thoughts
To start this final part of the project, I had to decide the bit size and type of data points that I was going to use. I chose to use 32-bit fixed-point hexadecimal for everything as this was the easiest option for the multiplication and keeping track of overflow and sign bits. My plan of attack for the structure of this project was to work from the neuron to the layers, to the final MLP neural network design. Inside the following subsections will be detailed explanations of the structure of the Verilog code and modules as well as their responsibilities in the final MLP design.
Neuron
The neurons responsibility is to handle the math of the neural network. This is where the adders and multipliers that were designed earlier in the project are going to be used for the equation below:
𝑜𝑢𝑡 = 𝑤1𝑖𝑛1 + 𝑤2𝑖𝑛2 + 𝑤3𝑖𝑛3 + 𝑤4𝑖𝑛4 + ⋯ + 𝑤𝑛𝑖𝑛𝑛 + 𝑏
The parameters for the neuron module are the weights file name, the number of weights, the number of outputs, the input, biases, and result of the product and summation of the bias. The result of the output is passed through the ReLU activation function module that was created earlier in this report. Below is the generative block loop that utilizes the carry look ahead adder and multiplier to create the sum of the product of the inputs and weights:
// Adding each product of the weights and inputs
generate
for (j = 0; j < num_weights; j = j + 1) begin: add
assign temp_sum = summation;
cla_adder add1 (
.sum(summation[31:0]),
.carry_out(carry_out),
.in1(results[j]),
.in2(temp_sum[31:0]),
.carry_in(carry_in));
end
endgenerate// Multiplying the weights, and adding the biases, against the respective data
fileread #(.file(file), .size(num_weights), .count(count)) weight
(.out(weights));
genvar i, j;
generate
for (i = 0; i < num_weights; i = i + 1) begin: multiply
cla_multiplier mul (.multicand(in[(31 + (32*i))-1:32*i]),
.multiplier(weights[(31 + (32*i))-1:32*i]),
.product(product),
.final(results[i]));
end
endgenerateLayer
The layer module is responsible for handling every neuron inside of that respective layer. I decided to only use one layer module and include parameters for its input and output sizes so that the hidden and output layer could be sourced from the same module. This is where the inputs, weights, and biases files will be declared for the neurons. Below is the generative loop block that creates each neuron inside of the layer depending on the input and output size of the layer:
generate
for (i = 0; i < num_out; i = i + 1) begin: layer
neuron #(.file(file), .num_weights(num_in), .num_outputs(1), .count(i)) n
(.in(image),
.bias(bias),
.result(outputs[i]),
.final(outputs[i]));
end
endgenerateFinal MLP
The final part of this project is the construction of the neural network that consists of the layer modules. This includes creating the hidden layer that feeds its output to the output layer for the final numerical 4-bit guess of the input. Below is the MLP module showcasing each layer and the guess output:
module mlpnet #(parameter input_file = "")(guess);
wire [31:0] outputs1 [(200)-1:0];
output [31:0] guess [(10)-1:0];
// Hidden layer, 784, 200
layer #(.file("hidden_weights.txt"), .num_in(784), .num_out(200)) hidden_layer(outputs1);
// Output layer, 200, 10
layer #(.file("output_weights.txt"), .num_in(200), .num_out(10)) output_layer(guess);
endmoduleResults
Because of the errors I had that caused me to turn this project in incomplete, I did not have many results to add to this section. The waveform below is the failed output from my neuron module testbench. This failure, I believe, was caused by the carry over of the multiplier module being incorrect.

Issues
I ran into a multitude of issues when completing the final stage of this project. Originally, as stated earlier in this report, I was going to be implementing a Convolutional Neural Network. I switched to the MLP because of my lack of knowledge with Verilog alongside having trouble building convolutions. Another problem I ran into was reading files using Verilog. The splicing method that I tried to use to combine all the file inputs into a single hex string was erroring due to the file reading method failing. This was solved by creating a temp 32 bit variable for storing the value before splicing into the final output.
The neuron module does not output a correct result. I believe this is due to the fact that the carry over bits in the multiplier module were inaccurate. I unfortunately could not solve this issue in the time of completing this report. This not working leads to the layer and neural network modules to fail because it is the backbone of these parts.
Conclusion
This project was extremely fun yet difficult. I believe that more experience using Verilog in prior classes would have benefited me, and probably other students, greatly in completing this assignment. I did not fully complete this project, but I firmly believe I was extremely close. In theory, my neuron, layer, and neural network modules should work if the bugs were ironed out.